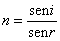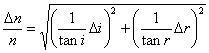Se realiza un simulación con multisim Implementando un circuito resistivo en serie con resistencias de valor el mismo valor para el cual con ayuda del multimetro se realiza una serie de mediciones de voltaje y corriente para cada punto respectivo.
miércoles, 12 de septiembre de 2012
RESISTENCIAS EN SERIE
Se realiza un simulación con multisim Implementando un circuito resistivo en serie con resistencias de valor el mismo valor para el cual con ayuda del multimetro se realiza una serie de mediciones de voltaje y corriente para cada punto respectivo.
martes, 11 de septiembre de 2012
PROCESO EXPERIMENTAL TEORIA DE ERRORES
Para el proceso de medición, fue necesaria la implementación del multímetro.
Se realizo bajo condiciones ambientales normales.
M1: 0.987
M2: 0.985
M3: 0.983
M4: 0.982
M5: 0.983
M6: 0.983
M7:0.984
M8: 0.984
M9: 0.991
Xmedia: 0.983
Varianza:
Vx² = 5,2521x10^-3
Desviación estándar:
D.e.= 0.0724713736
Valor Teórico:
Vt= 1Kohm ideal
∆x% = |(ValorTeórico – ValorExperimental)/ValorTeórico| = 1,67%
Ejemplo Extra sobre la aplicacion de estos principios : Un pediatra obtuvo la siguiente tabla sobre los meses de edad de 50 ninos de su consulta en el momento de andar por primera vez.
Calcular Varianza:
MEDIA ARITMETICA:
= 610/50= 12.2
= 7526/50 = -12.2^2= 1.68
Ejemplo Extra sobre la aplicacion de estos principios : Un pediatra obtuvo la siguiente tabla sobre los meses de edad de 50 ninos de su consulta en el momento de andar por primera vez.
| Meses | Niños |
| 9 | 1 |
| 10 | 4 |
| 11 | |
| 12 | 16 |
| 13 | 11 |
| 14 | 8 |
| 15 | 1 |
| xi | fi | Ni | xi · fi | x²i · fi |
| 9 | 1 | 1 | 9 | 81 |
| 10 | 4 | 5 | 40 | 400 |
| 11 | 9 | 14 | 99 | 1089 |
| 12 | 16 | 30 | 192 | 2304 |
| 13 | 11 | 41 | 143 | 1859 |
| 14 | 8 | 49 | 112 | 1568 |
| 15 | 1 | 50 | 15 | 225 |
| 50 | 610 | 7526 |
= 610/50= 12.2
VARIANZA:
= 7526/50 = -12.2^2= 1.68
TEORIA DE ERRORES
El resultado de toda medición siempre tiene cierto grado de incertidumbre. Esto se debe a las limitaciones de los instrumentos de medida, a las condiciones en que se realiza la medición, así como también, a las capacidades del experimentador. Es por ello que para tener una idea correcta de la magnitud con la que se está trabajando, es indispensable establecer los límites entre los cuales se encuentra el valor real de dicha magnitud. La teoría de errores establece estos límites.
De acuerdo con lo que hemos observado, y los datos obtenidos en los ejercicios, tenemos que cada vez que se efectúe el conjunto de operaciones requeridas para medir una determinada magnitud, se obtendrá un número que solamente en forma aproximada representa la medida buscada. Por lo tanto, cada resultado de una medición está afectado por un cierto error
De acuerdo con lo que hemos observado, y los datos obtenidos en los ejercicios, tenemos que cada vez que se efectúe el conjunto de operaciones requeridas para medir una determinada magnitud, se obtendrá un número que solamente en forma aproximada representa la medida buscada. Por lo tanto, cada resultado de una medición está afectado por un cierto error
Generalidades:
La teoría de errores es una ciencia fundamental para todas las materias donde se manejan y analizan grandes volúmenes de datos provenientes de observaciones directas o mediciones realizadas en laboratorio o trabajos de campo, tales como los que se desarrollan en topografía, geodesia, física, química y sobre todo estadística.
Esta ciencia, parte de la estadística, fue desarrollada por el matemático alemán Karl Friedrich Gauss a partir de sus estudios algebraicos y complementada luego por el inglés Sir Isaac Newton quien aplica su teoría del análisis matemático a la estadística y mas tarde por el francés Pierre Simon Laplace quien con su teoría de las probabilidades le da a la estadística y la teoría de errores carácter de ciencia.
Existen varios procedimientos para cumplir los objetivos de la teoría de errores, algunos incluyen procedimientos propios del análisis matemático, como integrales, derivadas, logaritmos Neperianos, etc. no parece ser necesario en estos apuntes tal profundización sobre un tema que no reviste capital importancia para las prácticas topográficas, por lo que solo se verá una versión básica del tema, que se adecua al tema predominante en el ámbito topográfico, la medición en todos sus aspectos. No obstante en el CD de este apunte se puede encontrar una versión mas completa de esta teoría, para quien quiera profundizar en el tema.
Cuando se efectúa la medición de una distancia para conocer su magnitud, solo se obtiene un valor aproximado de la misma, debido a variadas causas y efectos que afectan a todas las mediciones por lo que es imposible conocer con certeza y perfección la verdadera magnitud medida y el error que se ha cometido al hacerlo. Es objetivo de la teoría de errores hallar el valor mas cercano posible al verdadero de la magnitud que medimos y el error que hemos cometido durante el trabajo de campo.
Para ello se efectúa una serie de n mediciones de la magnitud a medir (donde n es un número entero, positivo y de un valor absoluto suficientemente grande como para alcanzar la precisión requerida por el trabajo a realizar). Estas nmediciones, en general, nos proporcionan magnitudes que difieren entre si por valores muy pequeños ya que los errores cometidos son, generalmente, pequeños y pasarían desapercibidos sino fueran objeto de observación. Al estudiar estos pequeños errores podemos, por medio de artificios matemáticos llegar a un valor tan aproximado al verdadero de la magnitud, y al error cometido, como se quiera.
Tenemos entonces por razones físicas, y también lógicas, dos premisas fundamentales obtenidas empíricamente:
- El valor exacto de una magnitud no se llega a conocer nunca.
- Siempre que se mide se cometen errores, es imposible evitarlos.
ACLARACION: En el lenguaje técnico utilizado el término << error >> utilizado repetidamente en esta unidad es sinónimo de vacilación o indeterminación, no de equivocación ya que estos sucesos, llamados errores groseros, no serán considerados en este estudio por su absoluta impredecibilidad.
Causas de los errores
Son numerosas pero solo nombraremos las mas importantes:
- Indeterminación de los extremos de la magnitud a medir ( por ej. el ancho de una calle sin líneas municipales perfectamente determinadas o el ángulo o la distancia determinada por dos señales muy gruesas).
- Limitaciones de nuestros sentidos, principalmente el de la vista, cuya acuidad visiva es de aproximadamente 00° 01' 00"; disminuyendo con la edad o enfermedades.
- Imperfección o inadecuación de los instrumentos utilizados, tanto por fabricación, malos
tratos, falta de mantenimiento, o razones económicas.
- Condiciones psicofísicas del operador como ser cansancio, estrés, enfermedades, apuro y por que no falta de responsabilidad o experiencia.
- Imprecisión intrínseca de los métodos de cálculo, como cuando se utilizan calculadoras y la cantidad de decimales no son suficientes para las precisiones requeridas.
- Condiciones atmosféricas adversas que puedan alterar los resultados de las mediciones.
Tipos de errores
Errores groseros o equivocaciones: Se deben a inexperiencia o irresponsabilidad del operador. En general su valor absoluto es grande y por lo tanto fácil de localizar dentro de una serie de mediciones. Las observaciones que han dado origen a estos valores se descartan ya que no pueden ser tenidas en cuenta para el cálculo pues harían decaer estrepitosamente la precisión.
Errores sistemáticos: Tienen su origen en causas permanentes y por lo tanto actúan siempre con el mismo signo y módulo. Son ocasionados por imperfecciones de los instrumentos, por factores meteorológicos o por la llamada "ecuación personal del operador" tendencia de cada operador a “redondear” las mediciones hacia abajo o hacia arriba, también forma de posicionarse frente al instrumento, acuidad visiva individual y formas características de bisectar, nivelar, etc.
En general se los puede calcular con suficiente precisión y por lo tanto anular. Tampoco son tenidos en cuenta para el cálculo.
Errores Accidentales: Son aquellos que responden únicamente a las leyes del azar, absolutamente fortuitos, se encuentran presentes en todo tipo de mediciones, pueden ser tanto positivos como negativos, y en grandes series tienden a anularse entre sí.
Por su imponderabilidad se los denomina también casuales o irregulares, y de ellos se ocupa fundamentalmente la teoría de errores.
No obstante su irregularidad cumplen con ciertas pautas como lo ha demostrado la experiencia, estas son:
- Los errores positivos y negativos de un mismo módulo se producen con igual probabilidad.
- Los errores pequeños se producen con mayor frecuencia que los errores grandes
Ejemplo sobre la aplicacion de la teoria de Errores:
Cuando tenemos que realizar procedimientos matematicos con medidas con error es muy util conocer claramente la teoria de error por ejemplo:
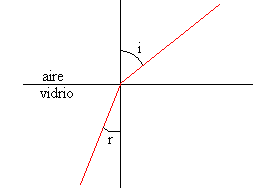 |
Cálculo del error en la medida del índice de refracción n.
|
Sea i=20±1 º y r=13±1 ºSe calcula el índice de refracción y el errorn=1.52
Δn=0.136Expresamos correctamente la medida y el error de nn=1.5±0.1

Suscribirse a:
Entradas (Atom)